In 2011, the Williams Institute at UCLA published an estimate of the lesbian, gay, bisexual, and transgender population of the United States. Reviewing various surveys and studies, the report estimated that about 0.3% of adults in the U.S. are trans. Since then, this figure has been repeatedly misquoted as “.03%”, often by conservative commentators who oppose trans rights.
Recently on Fox News, host Brian Kilmeade claimed that trans people are “.03 percent of the population”. Another recent story by Warner Todd Huston on Breitbart.com stated that “less than .03 percent of Americans are transgender.” A column by Joy Overbeck on Townhall.com is titled “The Tyranny of the .03 Percent”, although she later refers to “three-tenths of one percent of the population”. Brittany Hughes of the Media Research Center describes trans people as “less than .03 percent of the population”. Stella Morabito, who’s previously promoted hoaxes about “regret” after transitioning, also makes reference to “.03 percent of the population”.
Elsewhere, the incorrect “.03%” figure has been quoted by Tennessee state senator Mike Bell, Rod Dreher writing in The American Conservative, and pastor Greg Locke in Tennessee. Russ Sloan of the Daily Commercial even cited the “.03%” figure before referring to “the 99.7 percent” who “don’t consider themselves transgender”, and then quoted the “.03%” figure once again. It’s unlikely that all of these publications are referencing a separate estimate from another source – the Breitbart story cites an article from Livescience.com that includes the correct figure, 0.3%. These individuals are misreading and misrepresenting the size of the trans population by a significant factor.
A factor of 10 is a serious error
Some people may look at figures like 0.3% and 0.03% and think: they’re both such small numbers, does it really make that much of a difference? But decimal points and their placement do matter – you can’t just put them anywhere and expect that the meaning of a figure won’t be changed. 0.3 and 0.03 are two different numbers – 0.3 is 10 times greater than 0.03.
How great of a difference is represented by being off by a factor of 10? This is comparable to believing that Texas (268,596 sq mi) is roughly the size of West Virginia (24,230 sq mi). It’s the difference between driving from New York City to Philadelphia (97 miles), and driving from New York City to St. Louis (951 miles). A factor of 10 is the difference between drinking so much alcohol you’re over the legal limit, and so much you’re over the survivable limit.
Using a number that’s off by a factor of 10 can in some cases be fatal. These mistakes are so common in medication dosing that they’ve been termed “10-fold errors” by the medical field. Patients have died from accidental 10-fold overdoses of morphine, insulin, heart medications, and other drugs. Among these medication errors, mistakes involving the placement of decimal points can be the most common. In one study, 7 out of 64 residents at a pediatric hospital made 10-fold errors on a written test. Another study of real-life errors in dosage at a teaching hospital found that mistakes of decimal point placement were the largest category of dosage errors. These errors have been partly blamed on naked decimal points: numbers written without a leading zero before the decimal, like “.5”, can be misread as simply “5”. Those who make this mistake aren’t seeing where the decimal point is. People who read “0.3” and see “.03” are not seeing it either. This is a very serious error.
Alternatives for intuitive presentations of frequencies
The basic concept of proportions – the idea that there can be parts of a whole, and that these parts have sizes – is not very complicated. However, there are many different ways that proportions can be represented, and some of these representations can be more difficult to understand in certain circumstances. A number like “0.3” or “.03” gives the impression of a minuscule quantity – less than even a single unit. It’s easy for someone to treat this as a negligible remainder, something that can be dismissed as essentially a rounding error. One commentator described the “.03%” figure as “a mathematical zero” and “so small you can’t measure it”.
On top of evoking this sense of smallness, the expression of these figures as percentages creates additional complexity and room for error. For example: Cisgender Sally lives in a city with a population of 200,000 and wants to know approximately how many transgender people also live here. Trans people are 0.3% of the population. How should Sally use this information to find the number of trans people in her city? Take a minute to work out a solution before you continue.
Percentages are a kind of fraction, and 0.3% is the equivalent of:
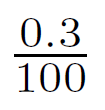
Sally can express this proportion without a denominator by dividing both 0.3 and 100 by 100:
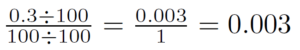
She can then multiply her city’s total population, 200,000, by this factor of 0.003, leading to an estimate of:
![]()
600 trans people.
There are several different ways to work out this problem – which one did you use? Sally’s approach requires applying various rules for decimal points, percentages, fractions, and specifically the multiplication and division of fractions. But most people simply won’t bother making the effort to walk through all these necessary steps upon seeing a figure that’s less than one percent. When they do, the number of operations required to achieve a more concrete understanding offers many more opportunities for mathematical errors, such as improperly multiplying or dividing the numerator or denominator, or otherwise misplacing one or more zeroes.
Any of these oversights can lead to a result that’s off by a factor of 10 or 100 or is otherwise incorrect. One study found that only 70% of U.S. citizens could correctly convert a figure of “1%” to the representation of 10 per 1,000. 30% of the population might not correctly understand figures expressed as percentages – so they may never reach a point where they recognize that the transgender population of the U.S. is larger than the populations of Boston, Washington D.C., Denver, or Seattle.
This confusion can be largely averted by expressing these proportions in a different format. Instead of requiring people to go through the error-prone process of understanding the meaning of 0.3%, we can present them with the end result: 300 per 100,000 people. These natural frequencies are more readily grasped than percentages – it’s easier to make estimates when you’re given information that allows you to add and subtract by groups of tens or hundreds, rather than requiring multiplication and division of fractions. For example: Cisgender Cindy, from a town of 90,000 people, can look at this figure and immediately understand that her city likely contains about enough trans people to fill an auditorium.
Again, the accessibility of these different representations can be very important: studies have found that physicians are much more likely to make correct calculations involving the accuracy of screening when they’re given figures expressed in natural frequencies rather than percentages.
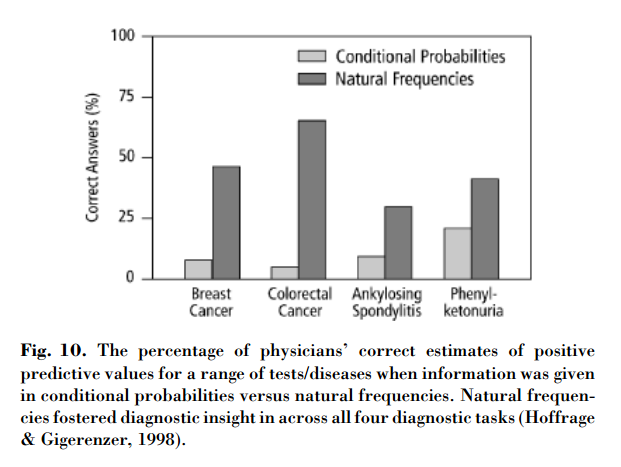
Gigerenzer et al., 2008
Natural frequencies are simpler to work with and convey a more practical sense of our numbers. Publications should consider expressing figures related to the transgender population in this format in order to communicate issues more clearly and minimize the likelihood of errors involving these numbers.
The public deserves accurate reporting
I write for a living, and I’ve previously edited patient reports, blog posts, and other publications for a medical startup. My work regularly goes through multiple layers of fact-checking that are meant to catch any errors in figures before they can go to press. I’ve been directly confronted with other errors of scale on live television – a CNN host claimed that hormone therapy can cost $100 a month, before I informed him that I was personally paying a quarter of that price out-of-pocket. It’s astonishing to me that so many high-profile media outlets will neglect to notice these glaring mistakes before splashing them across the headlines.
If publications and their writers are going to cover this topic, they have an obligation to present the public with accurate figures rather than misinforming their readers about the true size of the trans population. When it’s this obvious that they haven’t done the minimum of research and verification needed to ensure that their figures aren’t off by such a significant margin, it’s uncertain why they would feel they’re even qualified to discuss this. How can they know so little about something so basic, and yet continue to advance their narrow, invalidating, and hostile ideas about gender with such absolute certainty? How can you claim authoritative knowledge of biology, philosophy, and even the will of the divine, if you lack the knowledge of how to multiply and divide by 10? It’s already insulting to trans people that our rights, our genders, and our very lives are openly vilified and disparaged in the press. That insult is compounded when we are attacked by those who can’t distinguish between the numbers 0.3 and 0.03. ■




8 Responses to 0.3% is not 0.03%: representations of transgender frequencies in online publications (Gender Analysis 21)